Antoine Turquet

Quantifying location uncertainties in seismicity catalogs: Application to the Pyrennees.

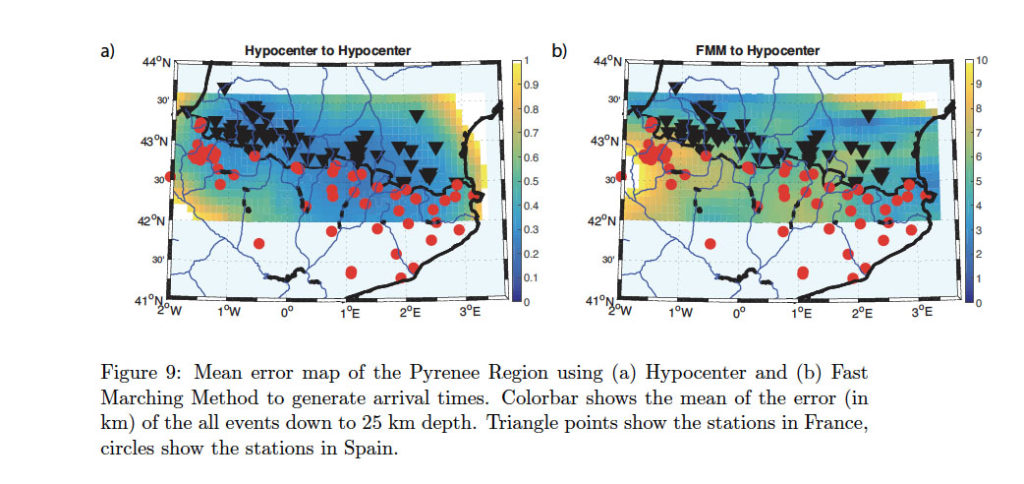
There are plenty of methods available for locating earthquakes. Linearised least squared optimisation methods are commonly used to construct seismicity catalogues, as they are fast and simple to implement. These methods are based on minimising the root- mean-square (RMS) of the travel time residuals to find best fitting location coordinates and origin time. There are two well known problems reducing the quality of estimation: (1) the linearisation of the inverse problem causes dependence on the initial guess, (2) regularisation of the velocity matrix gives solutions and eventually the error ellipses that can vary with the chosen damping coefficient. For example, one can artificially move the source position towards the initial guess location and decrease the size of the error by simply increasing the damping parameter. In this work, we propose a method to quantify unbiased uncertainties with a series of synthetic tests. We first generate travel times for events from all possible coordinates on a 3D grid and then locate each synthetic event by using HYPOCENTER software (this can be applied to any location method). Finally, we produce a 3D error map, where at each grid point, we plot the location error, i.e. the distance between the event at the given grid point and its inverted location. Furthermore, we show how this error map vary with the quantity and quality of data, and with user-defined parameters. We are also providing a methodology to tune the seismic location parameters and calculate the corresponding uncertainties for this set of parameters for the professionals who are using similar earthquake location softwares.